Universidad Autónoma del Estado de México. Plantel Dr. «Pablo González Casanova».

          Avance de proyecto Integrador Colaborativo. 

Problema de optimización usando la segunda derivada.

Asignatura: Cálculo Diferencial I.

Profesor: Víctor Eric Velázquez Núñez.

INTEGRANTES:

ESPINOZA JERÓNIMO MILDRED AMAIRANY.

GARCÍA ACOSTA JAVIER.

GUADARRAMA GUADARRAMA EDGAR HAFID.

MILLÁN DÍAZ JUAN CARLOS.

MILLÁN VAZQUÉZ DAVID ROBERTO.

OLMEDO MENDOZA MIGUEL ÁNGEL.

SEMESTRE: 5    GRUPO: 502

TENANCINGO, MÉXICO A; 27 DE NOVIEMBRE  DE 2018.

Teoría. 

*Optimización: Es determinar valores críticos de la variable independiente que hace que la función tenga un valor máximo o un valor mínimo.

*Variable independiente: Una variable independiente es aquella cuyo valor no depende del de otra variable. La variable independiente en una función se suele representar por x. La variable independiente se representa en el eje de abscisas.

*Derivada: Este se puede aplicar en problemas de optimización en los que se requiera calcular ganancias máximas, gastos mínimos, materiales mínimos, etc;  la mayoría de los problemas presentan dos condiciones (área y volumen), lo que nos permite hacer el cálculo de una variable y otra queda en función de la primera.

–Parte hecha por: Millán Vázquez David Roberto. 

Pasos para resolver ejercicios de optimización: 

1. Leer el problema para identificar los siguientes elementos: Datos del problema, condiciones del problema, comprender lo que se pide optimizar del problema.
2. Asignar las variables que usarás en el problema para plantearlo y resolverlo.
3. Realizar un dibujo de ser necesario, el cual te permitirá tener una visión más amplia del problema.
4. Plantear la función objetivo en término de las variables propuestas. Esta será la que te permitirá optimizar; puede quedar con dos variables.
5. Establecer una ecuación para cada una de las condiciones o restricciones del problema.

-Parte hecha por: Olmedo Mendoza Miguel Ángel. 

1. Despejar una variable de las ecuaciones que se generan en el paso 5.
2. Sustituir en la función objetivo generada en el paso 4.
3. Obtener máximos o mínimos de la función generada en el paso 7.
4. Concluir el problema y realizar una comprobación con los resultados obtenidos.

Criterio de la segunda derivada

Sea  una función y  uno de sus puntos críticos. Entonces,

• si , la función tiene un máximo en 
• si , la función tiene un máximo en 
• si , la función tiene un punto de inflexión en 

-Parte hecha por: García Acosta Javier. 

Problema.

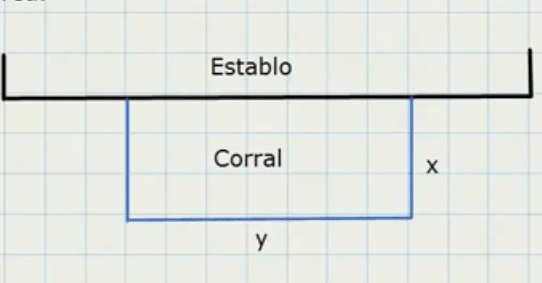
Un granjero tiene 120 metros de malla de alambre con la cual planea construir un corral al lado de su establo de 100 metros de longitud según la figura (el lado a lo largo del establo no requerirá malla de cerramiento). Cuales serían las dimensiones del corral que le darían la máxima área.

 –Parte hecha por: Millán Díaz Juan Carlos.

Procedimiento. 

Imagen del corral. 

-Guadarrama Guadarrama Edgar Hafid (procedimiento hasta el punto 5). 

-Parte hecha por Espinoza Jeronimo Mildred Amairany. (de la parte del procedimiento número 6 en adelante).